A large class of counting problems fall under the categories of 'permutation' and 'combination'. For example, almost all card games can be thought of as selecting permutations or combinations of cards. Since the field is so common, tools have been developed to simplify the counting.
What are combinations and permutations?
A permutation is a method of arranging all the elements from a collection in order.
A combination is a selection of elements from a collection.
For example, the number of ways you can draw 5 cards from a deck is a permutation. The number of 5 card hands is a combination.
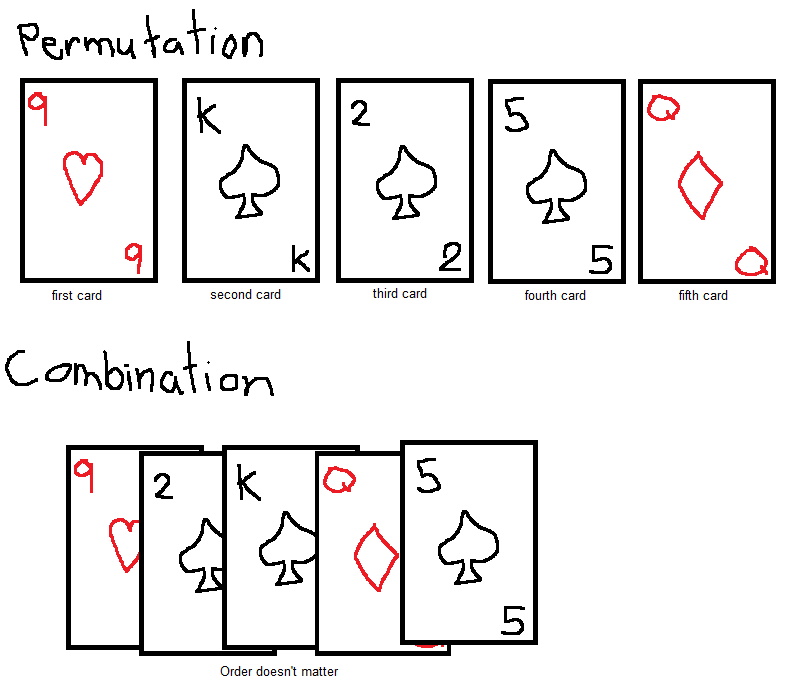
Counting permutations
Counting permutations is relatively simple. Look at the number of ways you have choosing the first element, then the second, then the third..., and since these actions are independent of one another, you simply multiply them to get the total number of permutations. The way we write this is:
\(_nP_r = \frac{n!}{r!}\)
Counting combinations
Combinations are bit trickier. Let's first ask: What's the relationship between combinations and permutations?
Let's think about a slightly different way of finding a permutation of elements. Say we're picking 5 cards from a deck. One way to do that would be to first pick they types of cards, and then, after having chosen them, pick an arangement.
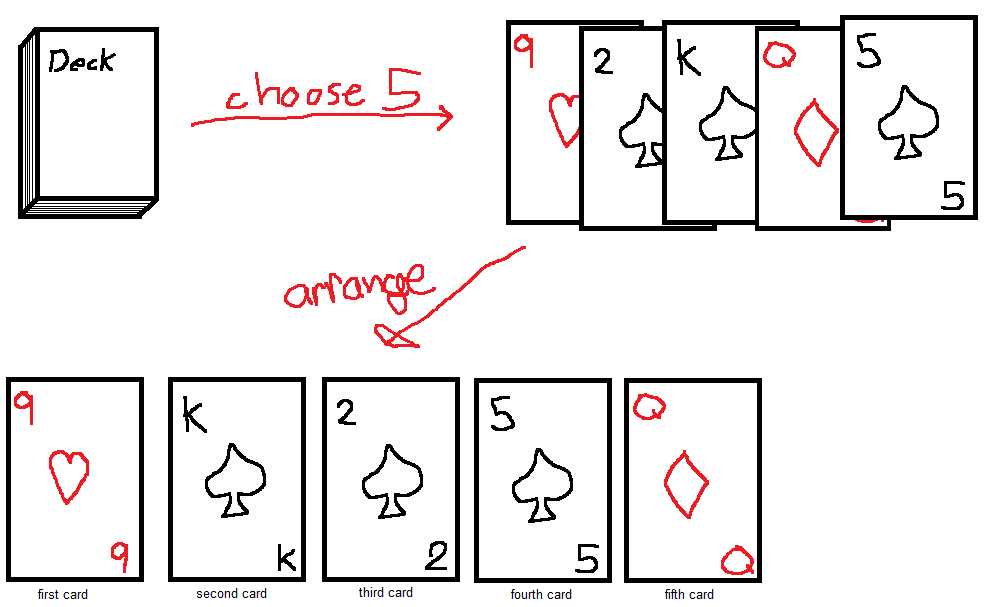
Notice that these two actions are independent of one another. That means that the total number of permutations is just the number of 5 card hands, multiplied by the number of ways we can order those 5 cards:
\(_{52}P_5 = [\text{Ways of choosing 5 cards}] * (_5P_5)\)
But look! The number of ways to choose 5 cards is exactly what we're looking for: the combination! Thus:
\(\text{Ways of choosing 5 cards} = \frac{_{52}P_5}{_5P_5}\)
We introduce a shorthand for "Ways of choosing 5 cards":
\(_{52}C_5 = \frac{_{52}P_5}{_5P_5}\)
In general, when choosing r elements from a collection of n elements, we write:
\(_nC_r = \frac{_nP_r}{_rP_r}\)
or
\(_nC_r = \frac{n!}{r!(n-r)!}\)
Wrapping up
The fundamental strategy for dealing with combination problems is first looking at the number of permutations and working backwards.